Raza cercului - Formula de calcul

Cercul este o formă geometrică fundamentală, definită ca mulțimea punctelor situate la aceeași distanță de un punct fix numit centru. Această figură are o importanță deosebită atât în matematică, cât și în viața de zi cu zi, fiind întâlnită în natură, tehnologie și artă. Proprietățile sale, precum raza, diametrul, circumferința și aria, sunt studiate încă din cele mai vechi timpuri, reflectând simetria și perfecțiunea acestei forme.Ce este raza cercului?

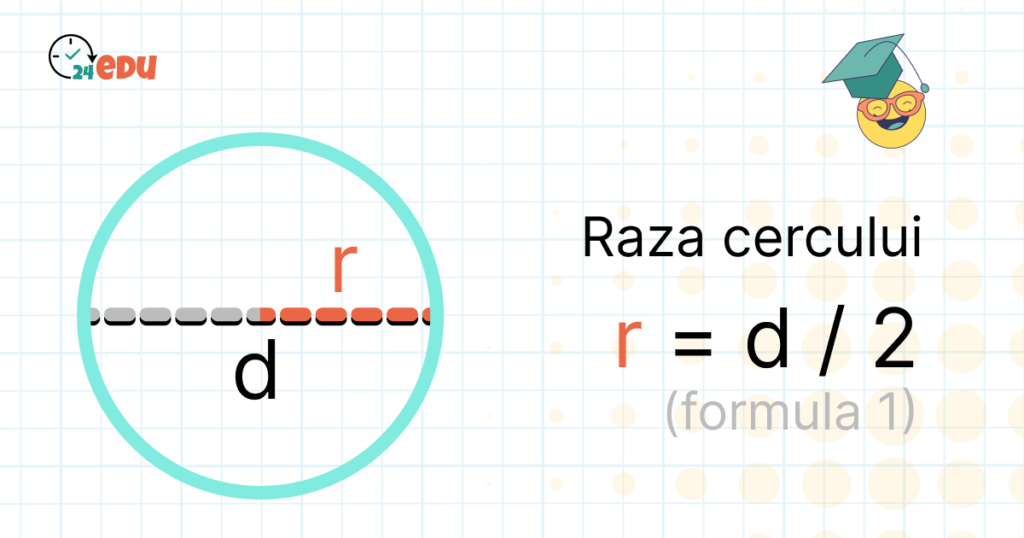
Ce este raza cercului?

Conform CueMath, raza cercului este segmentul de dreaptă care unește centrul cercului cu un punct de pe conturul acestuia. Reprezintă distanța constantă dintre centru și oricare punct de pe cerc. Este una dintre cele mai importante mărimi ale cercului, notată de obicei cu litera r, și stă la baza calculului altor proprietăți ale cercului, cum ar fi diametrul, circumferința sau aria.

Cum se calculează raza cercului?

Raza cercului se poate calcula în mai multe moduri, în funcție de datele pe care le avem:

Dacă știm diametrul (d): raza este jumătate din diametru
r = d / 2
Dacă știm circumferința (C): raza se calculează folosind formula
r = C / (2 × π)
Dacă știm aria (A): raza se calculează astfel
r = √(A / π)
Dacă avem un triunghi dreptunghic înscris într-un cerc (cercul circumscris): raza este jumătate din ipotenuză
r = ipotenuză / 2

Cele mai frecvente greşeli în calculul razei cercului

Se folosește diametrul fără a-l împărți la 2
Mulți confundă diametrul cu raza și uită că r = d / 2, ajungând astfel la o valoare dublă față de cea corectă.
Se uită pătratul în formula ariei
Când se calculează raza pornind de la aria cercului (A = π × r²), unii uită să aplice rădăcina pătrată după ce izolează raza:
r = √(A / π) – dacă nu se face radicalul, rezultatul va fi eronat.
Valori greșite pentru π
Se folosește o valoare prea aproximativă a lui π, cum ar fi 3 în loc de 3,14 sau 3,1416, ceea ce duce la o rază inexactă, mai ales în probleme cu unități concrete.
Greșeli de ordine a operațiilor
Împărțirea și extragerea rădăcinii nu se fac în ordinea corectă, ducând la rezultate greșite. De exemplu, dacă ai A = 78,5, trebuie mai întâi să împarți la π și apoi să extragi rădăcina.
Conversii greșite de unități

Se lucrează cu unități diferite (cm, m, mm) fără să se transforme corect, ceea ce afectează și valoarea razei.

Exemple de probleme cu raza cercului

Problema simplă cu diametrul

Enunț: Un cerc are diametrul de 12 cm. Care este raza lui?Rezolvare:
r = d / 2 = 12 / 2 = 6 cm

Problema cu aria cercului

Enunț: Aria unui cerc este 78,5 cm². Află raza, folosind π ≈ 3,14.Rezolvare:
A = π × r²
r² = A / π = 78,5 / 3,14 = 25
r = √25 = 5 cm

Problema cu circumferința

Enunț: Un cerc are circumferința de 31,4 cm. Care este raza lui? (π ≈ 3,14)Rezolvare:
C = 2 × π × r
r = C / (2 × π) = 31,4 / (2 × 3,14) = 31,4 / 6,28 = 5 cm

Problema aplicată

Enunț: O roată are raza de 20 cm. Ce distanță parcurge la o rotire completă?

Rezolvare:
Distanța parcursă = lungimea cercului = circumferința
C = 2 × π × r = 2 × 3,14 × 20 = 125,6 cm

Problema inversă

Enunț: Un cerc are o rază de 7 cm. Care este aria sa? (π ≈ 3,14)Rezolvare:
A = π × r² = 3,14 × 7² = 3,14 × 49 = 153,86 cm²

Alte linii importante în cerc

Într-un cerc, pe lângă rază, mai există și alte linii importante care joacă un rol important în geometrie:

Diametrul – este segmentul care unește două puncte de pe cerc trecând prin centru. Este cea mai lungă coardă posibilă și este egal cu de două ori raza.
d = 2 × r
Coarda – este un segment de dreaptă care unește două puncte de pe cerc, dar nu neapărat trece prin centru. Diametrul este un caz particular de coardă.
Arcul – este porțiunea de cerc cuprinsă între două puncte. Arcul poate fi minor (mai mic de jumătate de cerc) sau major (mai mare de jumătate de cerc).
Secanta – este o dreaptă care taie cercul în două puncte.
Tangenta – este o dreaptă care atinge cercul într-un singur punct. Este perpendiculară pe raza dusă în acel punct de contact.

Matematicieni care au scris despre raza cercului

Mai mulți matematicieni importanți din istorie au studiat și scris despre proprietățile cercului, inclusiv despre rază:

Euclid – considerat părintele geometriei, a scris în Elementele sale despre proprietățile cercului, definind noțiuni precum raza, diametrul și coarda.
Arhimede – a fost unul dintre primii care a studiat riguros cercul și a determinat relația dintre rază și aria sau circumferința cercului. El a oferit o aproximare foarte precisă a lui π.
Pappus din Alexandria – a continuat studiile lui Euclid și Arhimede și a oferit teoreme importante legate de geometria cercului.
Leonhard Euler – a contribuit la dezvoltarea analizei matematice și a introdus formule legate de cerc în contextul trigonometriei și geometriei analitice.
René Descartes – a pus bazele geometriei analitice, permițând descrierea cercului și a razei sale prin ecuații în planul cartezian.

Teoreme despre raza cercului – explicate detaliat

Raza este perpendiculară pe tangenta în punctul de contact
Această teoremă spune că, dacă se trasează o rază din centrul cercului până la punctul în care o dreaptă tangentă atinge cercul, atunci raza este perpendiculară pe acea tangentă.
Explicație: deoarece tangenta atinge cercul într-un singur punct, orice alt punct de pe tangenta este în afara cercului. Raza trasează cea mai scurtă distanță între centru și punctul de contact, deci formează un unghi drept cu tangenta.
Toate razele unui cerc sunt egale
Orice segment care unește centrul cercului cu un punct de pe contur are aceeași lungime.
Explicație: prin definiție, cercul este mulțimea tuturor punctelor aflate la distanță constantă (raza) față de centru. Astfel, nu poate exista o rază mai mică sau mai mare.
Diametrul este de două ori raza
Diametrul trece prin centrul cercului și unește două puncte de pe contur.
Explicație: diametrul este format din două raze coliniare, așezate cap la cap, deci lungimea lui este r + r = 2r.
O coardă este perpendiculară pe o rază (sau diametru) în mijlocul ei dacă și numai dacă este bisectată de acea rază
Explicație: dacă o rază sau un diametru intersectează o coardă în unghi drept (90°), atunci împarte acea coardă în două segmente egale și invers – dacă o coardă este tăiată în două părți egale de o rază sau diametru, atunci ele sunt perpendiculare.
Într-un triunghi dreptunghic, centrul cercului circumscris se află la mijlocul ipotenuzei
Explicație: într-un triunghi dreptunghic, ipotenuza devine diametrul cercului în care este înscris triunghiul. Raza este atunci jumătate din ipotenuză.

Curiozități despre aria cercului

Formula ariei cercului, A = π × r², a fost descoperită încă din Antichitate
Arhimede este cel care a demonstrat-o riguros, folosind metode geometrice ingenioase, cu mult înainte de apariția calculului integral.
Aria cercului crește proporțional cu pătratul razei
Asta înseamnă că dacă dublezi raza, aria devine de patru ori mai mare, nu doar de două ori.
Numărul π este infinit și neperiodic
Deși apare în formula ariei, π nu poate fi exprimat exact ca fracție și are un șir infinit de zecimale care nu se repetă.
Cercul are cea mai mare arie dintre toate formele cu aceeași lungime a conturului
Acesta este un rezultat celebru din calculul variational, cunoscut sub numele de problema izoperimetrică.
Aria cercului este legată de arii triunghiulare
Arhimede a arătat că un cerc poate fi „desfăcut” într-un triunghi cu baza egală cu circumferința (2πr) și înălțimea egală cu raza (r), deci aria devine (2πr × r)/2 = πr².
În unele culturi antice, aria cercului era aproximată greșit
Babilonienii și egiptenii foloseau valori aproximative pentru π, ceea ce ducea la formule inexacte – de exemplu, unii foloseau π ≈ 3,16 sau chiar 3.

Aplicații în care se folosește aria cercului

Calculul suprafeței unor obiecte circulare
Se folosește la determinarea suprafeței unor mese rotunde, roți, farfurii, capace sau oglinzi. Dacă știi raza, poți afla rapid cât spațiu ocupă obiectul.
În construcții și arhitectură
Se calculează suprafața fundațiilor circulare, a cupolelor sau a coloanelor. Este important pentru estimarea materialelor necesare sau a rezistenței structurii.
În agricultură
Se folosește pentru irigații circulare, unde o instalație de udare acoperă o zonă rotundă. Aria cercului ajută la estimarea cantității de apă necesară și a suprafeței irigate.
În proiectarea roților și a pieselor mecanice rotative
Se calculează aria pentru a înțelege forțele, masele sau echilibrul unei roți, de exemplu la automobile, biciclete sau turbine.
În electronică și tehnologie
Se aplică în proiectarea microcipurilor sau senzorilor cu formă circulară, pentru a calcula cât spațiu ocupă pe o placă de bază.
În urbanism
Se folosesc arii circulare pentru delimitarea unor zone de protecție sau influență, cum ar fi raza de acțiune a unei antene, unei camere de supraveghere sau a unei stații de metrou.
În educație și testări
Aria cercului este frecvent folosită în probleme de matematică, pentru exersarea conceptelor de suprafață, proporții sau ecuații.

Cum învață copiii mai ușor despre cerc?

Prin desen și decupare
Copiii pot desena cercuri cu ajutorul unui compas sau al unui obiect rotund (pahar, capac) și apoi să le decupeze. Astfel învață vizual și tactil forma cercului și elementele sale: rază, diametru, centru.
Folosind obiecte din jur
Roți, farfurii, mingi sau ceasuri sunt exemple concrete care ajută copilul să înțeleagă cum cercul apare în viața reală.
Jocuri și aplicații interactive
Aplicațiile educaționale, puzzle-urile sau jocurile de potrivire a formelor îi ajută pe copii să recunoască și să rețină cercul într-un mod plăcut și natural.
Experimente simple
De exemplu, măsurarea razei și a diametrului cu o riglă, apoi compararea lor, îi ajută să observe că diametrul este de două ori mai mare decât raza.
Povești și povești matematice
O poveste cu un personaj care se rotește, descoperă cercuri sau învață despre ele face procesul de învățare mai captivant.
Desen cu sfoară sau cu compasul
Folosirea unei bucăți de sfoară prinsă într-un cui sau bold, trasată în jur – este o metodă practică de a forma cercuri și de a înțelege noțiunea de distanță constantă față de centru.
Lecții scurte și clare, cu exemple concrete
Explicațiile simple, însoțite de imagini și întrebări, ajută la fixarea noțiunilor de bază, fără a încărca copilul cu termeni tehnici prea devreme.

Cele mai complexe moduri de utilizare a cercurior

Inginerie mecanică – roți dințate, turbine și piese rotative

În mecanica avansată, cercul joacă un rol central în proiectarea pieselor rotative, cum ar fi:

Roțile dințate: fiecare roată dințată are un cerc de divizare sau cerc primitiv, a cărui rază determină raportul de transmisie între două roți. Calculul razei este crucial pentru ca dinții să se potrivească perfect fără să alunece sau să sară.
Turbinele și rotoarele: în turbinele eoliene, hidraulice sau motoare cu reacție, raza rotorului determină puterea generată, deoarece cu cât raza e mai mare, cu atât se colectează mai multă energie cinetică din mediu.
Discurile de frână: în automobile, frânarea eficientă depinde de brațul de forță, care este practic raza discului. Astfel, inginerii optimizează raza pentru a asigura siguranță maximă fără a compromite greutatea.

Astronomie și astrofizică – modelarea corpurilor cerești

Deși orbitele reale ale planetelor sunt eliptice, cercul este important în modelele simplificate ale mișcării corpurilor cerești:

Distanța medie până la Soare este tratată ca raza unui cerc imaginar. De aici derivă calcule precum viteza orbitală, forța gravitațională sau energia mecanică totală.
În sistemele stelare binare sau în modelarea galaxiilor, cercurile sunt folosite pentru a descrie traiectorii stabile, unde raza exprimă distanța constantă dintre două obiecte aflate în echilibru gravitațional.
Cercurile apar și în eclipse: umbrele proiectate de Pământ și Lună sunt circulare, iar raza acestor umbre este calculată precis pentru a anticipa eclipsa totală sau parțială.

Tehnologia comunicațiilor – rază de acțiune și acoperire

În rețelele wireless, semnalul unei antene are o formă circulară de propagare (în plan orizontal). Aplicațiile includ:

Telefoane mobile și 5G: fiecare turn de telecomunicații acoperă un „celule” de formă circulară, cu raza definită de puterea antenei și obstacolele din zonă. Plasarea turnurilor se face astfel încât cercurile să se suprapună parțial pentru a evita „zonele moarte”.
Wi-Fi și rețele locale: raza semnalului este folosită pentru a estima numărul optim de routere și pentru a evita interferențele între ele. Unele dispozitive permit reglarea manuală a razei de semnal pentru a controla consumul de energie.

Navigație și geolocalizare – trilaterare și hărți GPS

Una dintre cele mai spectaculoase aplicații ale cercului este în GPS și poziționare geografică:

Un receptor GPS primește semnale de la cel puțin 3 sateliți. Fiecare semnal definește un cerc virtual, în care raza este dată de distanța până la satelit (calculată prin întârzierea semnalului).
Intersecția acestor cercuri dă poziția exactă a receptorului. Acest principiu se numește trilaterare, și este folosit și în sisteme de salvare, aviație, marină sau drone autonome.
Pe hărți digitale, funcții precum „căutare în apropiere” (restaurante, stații de încărcare, farmacii) se bazează pe o rază de acțiune circulară de la poziția utilizatorului.

Medicină și imagistică – reconstrucție 3D și scanare circulară

În domeniul medical, cercul apare în multe tehnologii:

Tomografia computerizată (CT) și rezonanța magnetică (RMN) folosesc raze X sau unde radio pentru a scana corpul în secțiuni circulare. Aceste secțiuni se reconstruiesc digital pentru a crea o imagine tridimensională a corpului.
În ecografie, senzorul generează unde circulare care se propagă în țesuturi. Timpul de întoarcere și intensitatea permit determinarea structurii interne a organelor, iar raza de acoperire a undelor influențează profunzimea scanării.
Chirurgia robotică și intervențiile minim-invazive folosesc ghidare bazată pe modele circulare pentru a menține instrumentele medicale la distanțe precise față de organe sensibile.

Arhitectură și design structural – cupole, teatre și acustică

Cercurile au un rol estetic și funcțional în arhitectura complexă:

Clădirile circulare (teatre antice, arene, rotonde) permit o distribuție uniformă a sunetului și o vizibilitate optimă. Raza scenei influențează direct acustica.
Cupolele și domurile, ca în cazul Pantheonului din Roma sau Bazilicii Sf. Petru, se bazează pe cercuri și sfere. Calculul razei de curbură este important pentru stabilitate, proporții și iluminare naturală.
În design urban modern, spațiile verzi sau piețele publice circulare sunt gândite pentru acces egal din mai multe direcții, raza fiind un indicator al accesibilității și funcționalității.

Realitate virtuală și interacțiune om-calculator

În VR, AR și jocuri:

Câmpul vizual (field of view) este descris printr-un unghi circular, cu raza corespunzătoare distanței de vizibilitate. Orice interacțiune în jurul utilizatorului se calculează printr-un „cerc de acțiune”.
În joystickuri sau trackpad-uri, mișcarea de rotație este interpretată prin coordonate polare (rază și unghi), ceea ce permite controlul fin în medii 3D.
Jocurile strategice sau de supraviețuire folosesc zone circulare de influență, atac, sau protecție, unde raza determină gradul de risc sau avantaj tactic.

Cercul este una dintre cele mai importante și fascinante forme geometrice, cu proprietăți simple, dar profunde. Prin elemente precum raza, diametrul sau aria, el stă la baza multor aplicații practice și descoperiri matematice. Înțelegerea cercului, încă din copilărie, dezvoltă gândirea logică și oferă o fundație solidă pentru studiul geometriei mai avansate.

Raza cercului – Formula de calcul